Analysis of DeepSeek v3 and Llama 3

DeepSeek had a big release last week with their DeepSeek-v3 671B parameter MoE model, alongside an excellent paper detailing a wide array of system optimizations. Among these, their efficient training economics, success with FP8, and network-aware MoE stood out to me most. We will use Meta’s Llama 3 405B as a main reference point for the analysis¹², as one of the most recent and largest other open-paper/architecture models with comparable quality. Just to be clear, I have no affiliation with either party and such a post is only enabled by extremely high-quality work and documentation by both parties. Let’s dive in!

Preliminaries

In what follows, when we say “pre-training” we will refer strictly to the initial pre-training stage- we omit DeepSeek’s two subsequent context-extension stages (to 32K, then to 128K) and Llama’s context extension (to 128K) and learning rate annealing stages; in both cases, the combined subsequent stages took up ≈5% of training cost/token count. Also, FLOPs should be read as “floating point operations” and FLOP/s as “floating point operations per second”. Lastly, for FLOP calculations, I assume both parties use attention kernels with causal masking, so the number of operations is halved compared to full attention.

Training Economics

Let’s compare pre-training cost in GPU hours. For DeepSeek, this is reported as 2.7M H800 hours. For Llama, we can back it out: with 8K sequence length, 1 token needs ≈2.54 TFLOPs³ so 15.7T tokens needs 41.4T TFLOPs (double T); estimating their average BF16 MFU as 42% with H100 peak BF16 TFLOP/s as 990 gives 416 TFLOP/s; so we get 27.6M H100 hours. Note this may be a slight overestimate, as Llama masks attention between documents in the same 8K window, but even 1K average document length reduces total cost by only ≈4%, as FFN size > hidden size > 8K window » 1K window for Llama.

One ambiguous factor that’s worth noting is hardware failure. The Llama paper reports 419 unexpected and 47 expected failures/interruptions during a training snapshot of 54 days. It seems unlikely the reported ≈42% MFU is on aggregate, accounting for these failures. However, DeepSeek doesn’t provide any data on this, so we proceed assuming equal failure rate in GPU hours, so the relative factors cancel out.

How to properly normalize between H800 and H100 hours is less clear. There appears to be at least two H800 80GB specs and two H100 80GB specs- H100/800 PCIe and H100/800 SXM5, with the pair of PCIes and pair of SXM5s each having the same peak (non-FP64) TFLOP/s⁴⁵⁶. PCIe has 25% lower peak TFLOP/s than SXM and 50% lower max TDP. Based on memory specs from their paper, Meta likely used H100 SXM5, whereas it’s unclear for DeepSeek but where applicable we’ll assume the seemingly more common H800 PCIe. For intra-node network, both use NVLink, but DeepSeek reports 160 GB/s, far from the 400 GB/s seen on some specs for H800 PCIe, and even more so from the headline 900 GB/s in NVLink 4.0 that comes with H100 SXM5⁷⁸. One commonality between the two setups is 50 GB/s inter-node network, exclusively IB for DeepSeek and IB/RoCE for Meta. All this is to say, we can’t directly compare training costs, but we do know Llama took 10x the H100 hours than DeepSeek did H800 hours, and we could guess 1 H800 hour = 0.75 H100 hours. Taking all the reported numbers at face value, this suggests 13x savings in pre-training compute on DeepSeek’s part to produce a model of comparable quality. Where do these savings come from?

To answer this, we’ll breakdown DeepSeek’s model architecture, mixed-precision computation, and network co-designed parallelization strategy.

Model Architecture

There are several architectural differences between the DeepSeek and Llama models:

Mixture of Experts with a shared expert akin to a mini non-MoE MLP and selectively activated routed experts
Multi-Latent Attention with low-rank down and up projections for Q, K, and V and separate RoPE for Q and K, followed by standard Multi-Head Attention
Multi-Token Prediction with shared embedding and output head, and new projection and transformer block, for each future token. They use 1 MTP module for the 1st token after original prediction. The projection takes the concatenation of previous module representation and corresponding token’s embedding as input, and we assume the per-future-token Transformer block to be the same as the rest in the main model. While the paper specified placement of the embedding, output head, and MTP module in the same Pipeline Parallel rank, it didn’t specify if they managed to compute the embedding lookup per token only once for both uses- main model forward and MTP forward (note this question doesn’t apply to the output head, as the main model and MTP’s last activations differ). It seems more likely than not that they did, so we’ll assume that.

With the aforementioned assumptions, here’s the breakdown of DeepSeek’s TFLOPs per token into different architectural components, all precision-agnostic (for now). Note that DeepSeek doesn’t apply inter-document intra-window attention masking, so there’s no uncertainty from that factor unlike in Llama.

Component	TFLOPs/token
Main Model + MTP MLA without attention*	0.070
Main Model + MTP attention*	0.031
Main Model + MTP MoE	0.148
Shared Embedding & Output, MTP Projection	0.017
Total	0.266

Note: “attention” refers to just Softmax(QK^T/sqrt(d))V, no other input or output projections.

Comparing the two models, we see that DeepSeek requires ≈10.5% of the FLOPs per token that Llama does, and with 6% fewer tokens, ≈10% of (main) pre-training compute in FLOPs. The 10.5% may seem surprising, but with an active parameter ratio of 37B:405B, it roughly checks out. With all experts active, the MoE TFLOPs would be 4.21, bringing the total per token to 4.33, and 671:405 ≈ 4.33:2.5. DeepSeek also performs selective recomputation during backprop for MLA up-projections and the SwiGLU in MoE (and RMSNorm but we don’t count that)- accounting for that boosts per-token “nominal” TFLOPs count by 0.038 or 14% to 0.304. However, for clarity and fair comparison, we will stick with the “effective” 0.266.

So, of the roughly 12.5x compute savings, we can attribute ≈10x directly to fewer FLOPs. Perhaps a better-grounded perspective is that, since DeepSeek’s 10x GPU-specific hours savings almost exactly cancels their 10x FLOPs savings, they essentially neutralized their presumable disadvantage (to whatever unknown extent it is) in compute infrastructure to achieve equal net TFLOP/s. An obvious and important question is how comparable model quality was achieved with 10x fewer FLOPs, and as discussed thus far these are precision-agnostic FLOPs- the ratio is even more lopsided when considering DeepSeek’s use of FP8 with potential precision loss. Although we won’t discuss this further here, DeepSeek does introduce several optimizations to curtail precision loss, including fine-grained block quantization and high-precision accumulation on CUDA Cores. Nevertheless, we will focus on their system efficiencies to overcome the hardware disadvantage.

Mixed-Precision Computation and Communication

As alluded to, one key ingredient in DeepSeek’s efficiency gains is mixed-precision training. Whereas Llama deploys BF16 everywhere, DeepSeek uses BF16 GEMMs only for embedding, output head, MoE gating, and attention, and FP8 elsewhere- this comes out to only 18% of FLOPs in BF16! At first glance, if we assume equal tensor core utilization, this would suggest a ≈82% speedup or 45% time savings in computation, which almost makes DeepSeek neutralizing the infrastructure disadvantage underwhelming. However, one hypothesis as to why DeepSeek’s efficiency gains are not that large, without making assumptions about kernel efficiency, is that they don’t quantize communication as aggressively, and thus it becomes a bottleneck.

To validate or invalidate this, we first detail our interpretation of DeepSeek’s training parallelization strategy in the figure below, with arrows indicating forward activation flow (apologies for both 0-indexing and 1-indexing, it felt right).

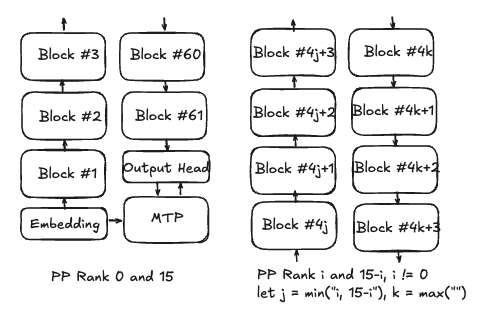
Figure 1: Proposed DeepSeek Pipeline Parallelism Strategy

In particular, given that PP=16, their DualPipe PP strategy is described as bidirectional, and there are 61 main model Transformer blocks, we assume the first and last PP ranks have Embedding, Output Head, MTP Module (projection + block), and 5 blocks, whereas the rest have 8 blocks. There are two nice properties with this strategy, one general to bidirectional pipelines and the other specific to DeepSeek’s model specs. Unidirectional PP strategies like 1F1B suffer from uneven activation memory footprint between ranks, as in the extreme comparison the first rank needs to store activations for all in-flight microbatches, whereas the last rank immediately consumes the activations of its current microbatch with the immediate backward pass, and for most schedules we can linearly interpolate to estimate relative memory consumption for any intermediate rank. Bidirectional PP is more balanced due to first and last colocated, second and second last colocated, etc. A separate source of memory imbalance is in assigned parameters to PP ranks, in particular with the first and last getting the oft-larger embedding and output head, respectively. With DeepSeek’s specs this appears to no longer be a problem and in fact the trend reverses- with each block (and MTP) holding roughly 11.5B parameters whereas embedding and output head combined holding 2B parameters, so we get around 60B parameters for the zero PP rank and 92B parameters per non-zero PP rank, thanks to the large number of experts. (note: take these and all numbers with some error bars- based on the calculations used here, I ended up with 715B total parameters including MTP, a bit more than the reported 671B parameters, which would only be boosted to 680B if not originally counting MTP). Holding model size constant, this scenario is preferred over the aforementioned one, as the maximum memory consumption across all ranks is lower and thus less of a bottleneck. However, if all the assumptions and steps here are correct, one can’t help but wonder why not fit another two transformer blocks into the main model? This can marginally be explained by the embedding and output head being kept in BF16 with nearly all other weights in FP8, but there still remains a significant gap in footprint between the PP ranks.

Now we can analyze the distribution of precisions used in GPU memory transfers in DeepSeek relative to Llama’s baseline of all BF16 besides weight gradients in FP32. Our model of DeepSeek’s model at a block granularity for a single GPU is shown below, with arrows indicating forward activation flow.

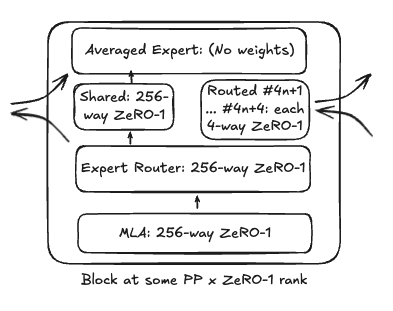
Figure 2: Proposed DeepSeek Transformer Block Parallelism Strategy

The notable assumption here is optimistic application of ZeRO-1 wherever it can fit, which may be going overboard for some parts of the model (read: the optimizer state for the router per block going from 7168x256 to 7168x1), but those parts have negligible footprint regardless. Further, due to the bidirectional pipeline, we count the opposite ranks in the same PP group to also be in the same FSDP group- this explains why despite 2048 GPUs with 64-way EP and 16-way PP suggesting 2-way ZeRO for experts, we actually label it as 4-way (and likewise multiply by all the block’s layers’ ZeRO degree by 2). Due to ZeRO-1, we can break inter-GPU transfers into three categories: activations, gradients, and weights. While DeepSeek has both forward and recomputed backward activations, the latter consists of device-isolated RMSNorm, MLA up-projection, and SwiGLU which individually don’t require communication. In fact, the only communication is from ZeRO (as short for ZeRO-1) to EP, then back from EP to ZeRO, and point-to-point between PP stages. Of these three types, only ZeRO to EP transfers are described as done in FP8, and the rest in BF16. For gradients, we have the same three types for activation gradients, again with only ZeRO to EP (this time backwards) in FP8, as well as weight gradients reduce-scatter in FP32 like Llama (note: gradient reduce-scatter is technically only used in ZeRO-2, but appears to this author as free lunch over the gradient all-gather in ZeRO-1, so we assume DeepSeek used it). Finally, the all-gather for weights follows the same split between FP8 and BF16 as was used for GEMM breakdown.

However, there’s further complication with DeepSeek’s network-aware MoE, which constrains the number of nodes with any activated experts for each token, and sends the token activation to at most one GPU in another node (which can then route it to several intra-node GPUs). So we further distinguish between intra-node and inter-node transfers. Following the implied setup of each node being contained within a PP stage, the PP transfer sizes should be exact, whereas EP-related transfer sizes are expectations assuming uniform distribution over expert relative rank. These numbers are all per DeepSeek’s 15360 batch size, should be independent of potential gradient accumulation, and account for the custom networking strategy for MoE.

Category	Type	FP8		BF16		FP32
Category	Type	Intra	Inter	Intra	Inter	Intra	Inter
Activations	ZeRO to EP	391 TB	196 TB
	EP to ZeRO			391 TB	196 TB
	PP				13.5 TB
Activation Gradients	ZeRO to EP	391 TB	196 TB
	EP to ZeRO			391 TB	196 TB
	PP				13.5 TB
Weight Gradients	ZeRO reduce-scatter					0.0 TB	2.2 TB
Weights	MoE/MLA ZeRO all-gather	0.0 TB	0.5 TB
Weights	Embedding/Output/Gating ZeRO all-gather			0.0 TB	0.0 TB

As expected, EP dominates, followed by PP, followed by ZeRO. A primary reason why ZeRO requires much less communication than the cheap point-to-point PP is that the ratio of communication between latter and former scales linearly in global batch size, and DeepSeek’s 15K batch size appears relatively large- 7x larger than Llama’s 2048 (albeit with half the sequence length). If we time-weight the inter-node communication by the 3.2x differential DeepSeek suggests, the rounded final split is 49% FP8, 51% BF16, and 0% FP32. So indeed DeepSeek quantizes communication less aggressively, but 50% is still quite high, and if they hypothetically began from a fully overlapped computation-communication ratio, we would expect them to now be communication-bound, but around 50% more efficient, which is likely more than the per-GPU differential between H100 and H800.

To get a better picture, let’s take a look at Llama’s communication distribution based on their 3D parallelism of TP, PP, and custom FSDP (ZeRO-2 + no resharding weights between forward and backward). Note that CP is only introduced in context extension which we don’t discuss here, and of the 8K and 16K Llama training compute sizes, we will just analyze the 16K case (it only affects FSDP transfers which as we’ll see are negligible). The transfer categories and types within them are now: activations, with TP in each layer and PP between stages; activation gradients, the same but backwards; weight gradients, reduce-scattered like in DeepSeek, and weights, now all-gathered and reduce-scattered once per global batch. All are in BF16 besides weight gradients in FP32. Here are the numbers with Llama’s 8K sequence length and 2K batch size (and this time the computed Llama model size did agree with the reported 405B parameters).

Category	Type	BF16		FP32
Category	Type	Intra	Inter	Intra	Inter
Activations	TP	970 TB
Activations	PP		8.2 TB
Activation Gradients	TP	970 TB
Activation Gradients	PP		8.2 TB
Weight Gradients	FSDP reduce-scatter				1.6 TB
Weights	FSDP all-gather + reduce-scatter		1.6 TB

We can use these numbers to compare total training communication volume. Using their respective total token counts, we get 552 EB for DeepSeek and 1822 EB for Llama, or roughly 3.3x more for Llama. If we account for interconnect bandwidth and assume 100% interconnect utilization, taking Deepseek’s reported 160/50 intra/inter-node GB/s, Meta’s reported 50 inter-node GB/s, and assuming Meta has 900 intra-node GB/s, the theoretical total (possibly double-counted due to overlap) pre-training communication time for DeepSeek is more than 2x that for Llama. We had determined earlier that Llama requires 10x more precision-agnostic FLOPs, and assuming comparable kernel efficiency across precisions this balloons to 18x more precision-weighted FLOPs. To reason about this large discrepancy between compute and communication ratios, let’s take a closer look at the EP-based MoE in DeepSeek, and then compare with TP in Llama, the sources of 96% and 99% of respective communication.

Networked MoE

During training, the routed portion (shared is much smaller and needs no communication so we omit discussion) of DeepSeek’s MoE can be broken down into:

Computation (all FP8)
- Locally routed expert computation
- Intra-node routed expert computation
- Inter-node routed expert computation
Intra-node Communication
- Intra-node routed inputs (FP8)
- Intra-node routed inputs from different relative-rank inter-node (FP8)
- Intra-node routed outputs (BF16)
- Intra-node routed outputs for different relative-rank inter-node (BF16)
Inter-node Communication
- Inter-node routed inputs (FP8)
- Inter-node routed outputs (BF16)

“different relative-rank” refers to the ultimate source and destination being on different nodes with different relative ranks in their node. The inter-node communication itself is always between devices with equal relative-rank. Let’s first get estimates for how long each of these take per device in forward, using 15360 global batch size, the previous 256-way DP assumption, and no gradient accumulation (DeepSeek does use gradient accumulation but it’s only a constant factor change to all following calculations) to get 60 local batch size with 4K seqlen still. We assume 100% bandwidth utilization, use the H800 PCIe spec, and since DeepSeek uses 20/114 SMs for communication, we estimate 85% * 94/114 = 70% GEMM utilization or 1059 FP8 TFLOP/s. We take expected values justified by the law of large numbers to get token counts, estimate each token routes to 3.93 unique nodes (possibly it’s own), and replace the 4 experts per device with 1 (but otherwise same numbers for expert dim, top-k nodes, top-k experts, etc), which should not affect any expected values.

Category	Type	Time (ms)
Computation	Locally routed	2.56
	Intra-node routed	17.89
	Inter-node routed	143.08
Intra-node Communication	Intra-node routed inputs	9.63
	Intra-node routed inputs from different relative-rank inter-node	67.44
	Intra-node routed outputs	19.27
	Intra-node routed outputs for different relative-rank inter-node	134.87
Inter-node Communication	Inter-node routed inputs	123.31
Inter-node Communication	Inter-node routed outputs	246.62

This gives totals by category of 164, 231, and 370 ms. As a sanity check, the 3.2x slower interconnect but 2x fewer tokens should give 1.6x more total comm time for inter-node vs intra-node, and 1.6 x 231 ≈ 370. Theoretically, the minimum time would be obtained if the inter-node interconnect was always utilized and local comp / intra-node comm was never exposed. Since local comp < intra-node comm, we’ll try to achieve this through a hierarchical pipeline: first overlap local comp fully with intra-node comm, then overlap intra-node comm fully with inter-node comm. Letting GPU i,j be the j-th GPU on node i, we introduce the following atomic units for stages in our pipeline: G(k,l -> i,j), tokens from i,j with expert GEMMs done on k,l, F(i,j -> k,l), FP8 intra-node communication of token inputs from i,j to k,l, and B(i,j -> k,l), BF16 intra-node communication of token outputs from i,j to k,l. Coincidentally, the F/B naming for FP8/BF16 can also be read as Forward/Backward, which we’re used to seeing in PP stages and also have the same 1:2 ratio. For F and B with i != k, we assume necessary inter-node is already done and just include intra-node time. From the table, G(i,j -> k,l) takes 2.6 ms, F(i,j -> k,l) takes 9.6/7 = 1.4 ms, and BA(i,j -> k,l) takes 1.4*2 = 2.8 ms, for all i,j,k,l due to LLN. If we lax G to 2.8 ms (which we have several justifications for, eg little below 85% utilization of available cores), we have a 2:1:2 ratio and here’s one possible fully overlapped intra-node pipeline for GPU i,j (why the G’s are unaesthetically packed will become clear soon):

Figure 2: Proposed DeepSeek Intra-Node MoE Pipeline

In case the text is too small, those are + and - between j and the number, all mod 8. Note that this pipeline reused i, suggesting intra-node token origin, and can coincide with identical pipelines for other intra-node GPUs without contention, assuming the same start time. Further, we could swap node i for node k in the first argument of G and second argument of F/B, to represent all intra-node work done at node i for tokens of node k origin. So, we can represent this full intra-node pipeline as a stage G(k->i) in the next pipeline between intra and inter-node. We introduce analagous stages F(i->k) and B(i->k) for FP8 inter-node communication for tokens from node i to node k and BF16 inter-node communication for token outputs from node i to node k. G(k->i) takes 7*(2.8+1.4) = 29.4 ms, F(i->k) takes 123.3/7 = 17.6 ms, and B(i->k) takes 17.6*2 = 35.2 ms, for all i,k. Since G < B, we can reuse a similar pipeline with relatively smaller G’s and updated labels (extra space between third and fourth G’s is not meaningful):

Figure 3: Proposed DeepSeek Inter-Node MoE Pipeline

So, at least theoretically, we can always utilize inter-node interconnect with no exposed local comp / intra-node comm for forward MoE. What changes with backward? All the communications just reverse direction and since everything is symmetrical, the communication stage sizes are unaffected. The main change is the addition of weight gradients- we now have double the computation (we’ll call these W stages) in the intra-node pipeline. However, the only scheduling constraint for the W stages is they must come after corresponding F, but not necessarily before corresponding B. Here’s what one maximally overlapped intra-node pipeline could now look like:

DeepSeek Intra-Node MoE with Weight Gradients

Figure 4: Proposed DeepSeek Intra-Node MoE Pipeline with Weight Gradients

For the inter-node pipeline, G(k->i)’s time needs updating to 16 * 2.8 = 44.8 ms. We won’t draw it out, but we can check whether a similar pipeline with 8 F’s of 17.6 ms followed by 8 B’s of 35.2 ms can fully overlap 8 G’s of 44.8 ms. Since the initial local G has no dependency, and each G thereafter is longer than corresponding F, the last G can finish at soonest after 8 * 44.8 = 358.4 ms. In contrast, to fully overlap communication with no gaps, the last B must begin after all other F and B, so 7 * 17.6 + 6 * 35.2 = 334.4 ms. We come up a little short, so with the current numbers/pipeline, there’s a small exposure of intra-node work. But, recalling our previous 2.6 -> 2.8 nudge in GEMM time, if we were to undo that now that GEMM is the intra-node bottleneck, we would instead get 358.4 * 2.6/2.8 = 332.8 ms . Of course, meeting an estimated threshold by an estimated value after an estimated adjustment isn’t in and of itself meaningful. But as long as this analysis is roughly correct, the bottom line is that DeepSeek’s MoE hyperparameters- including hidden dimension, expert dimension, and number of total and routed experts- were perfectly designed to fully overlap communication with backward computation. In the paper, they alluded to being able to support up to 3.2*4 = 13 experts with the same communication cost- perhaps the reason they chose 8 instead was because beyond that network was no longer the bottleneck.

One potential concern with the proposed hierarchical “BFS” pipeline is activation memory, as per GPU we accumulate all the activations from intra-node ranks during the intra-node pipeline. In the worst case of co-occurrence of all BF16 outputs from one node and all FP8 inputs from the next (in inter-node pipeline terms) node, we get around 3 * 60 * 4096 * 7168 = 5.3 GB in (mixed-precision) activations per GPU. However, just the up-projected key activation in MLA is 60 * 4096 * 128 * 192 = 6 GB, so the maximum memory consumption shouldn’t be higher for the pipelined MoE. Note that the comparison is for relative numbers not absolute, as they used gradient accumulation so these numbers are a constant factor too large.

Our original motivation was to ascertain DeepSeek’s much higher communication requirements than Llama. We can now see that, of the 96% of total communication time that is attributed to EP, accounting for overlapping intra-node and inter-node brings it down by 1/2.6 = 38%. Of the remaining 62% that is inter-node communication, 50% is completely overlapped with backward expert GEMMs, and the other 50% has only (10.5-8)/10.5 = 23% exposed. So the real exposed EP communication time is 7% of the listed EP time above. This also explains the motivation behind their DualPipe strategy for eliminating exposed PP- after their MoE optimizations- an unoptimized PP would account for ≈33% of communication. Let’s now compare with TP in Llama.

Although there have been several recent works on asynchronous TP, the Llama report only mentions asynchronous PP and FSDP, so we’ll proceed assuming synchronous TP. In particular, since the all-reduce in attention must be done between the out projection and subsequent MLP block, and similarly the all-reduce after down projection must be done before next layer’s attention block, TP is fully exposed. We don’t discuss the other two parallelisms due to relatively minimal overhead. So despite the estimate 2:1 ratio for total communication time in DeepSeek vs Llama, the ratio for exposed communication time is between 1:5 and 1:7, depending on the effectiveness of DeepSeek’s DualPipe.

Recap

In sum, we began by determining DeepSeek pre-training required 10x fewer GPU-specific hours than Llama. We then found that FLOPs spent based on architecture and dataset size equalizes efficiency besides the gap in Meta H100 hour vs DeepSeek H800 hour. After accounting for significant use of FP8 precision on DeepSeek’s part for both GEMMs and communication vs pure BF16 for Llama, on paper it appeared that DeepSeek had even more precision-normalized FLOPs savings, but roughly 2x more communication time, the latter particularly exacerbated by their weaker NVLink. Yet, after taking a closer look at the overlap in computation, intra-node communication, and inter-node communication in the MoE, we found that over 90% of the purported communication could be hidden, and in this process discovered potential answers for some of DeepSeek’s architecture design choices, such as their choice in number of routed experts per token.